티스토리 뷰
programmers.co.kr/learn/courses/30/lessons/68937
코딩테스트 연습 - 트리 트리오 중간값
5 [[1,5],[2,5],[3,5],[4,5]] 2
programmers.co.kr
- 접근법
이 문제에서 가장 중요한 것은 중간값의 의미를 평균값으로 오해한다면 자칫 문제가 더 어려워진다..
문제의 예시에서 나오는 세 값중의 중간값, 즉 정렬된 값 A,B,C가 있다면 중간값은 B이다.
따라서 각 A,B,C의 값은 정점(A,B,C)가 있다면 (A-B거리, A-C거리, C-B거리) 이다.
또 여기서 주어지는 값은 트리를 형성한다. (사이클이 없다, 간선의 수는 정점의 수-1)
그렇기 때문에 각 정점 사이의 경로는 '유일' 하다.
위 조건들을 가지고 다시 문제를 보면, 결국 답을 얻기 위해 우리가 노력해야할 것은
임의의 정점 A,B,C 에서 A-B,A-C,C-B의 거리 중 최소한 2개는 가장 크게 만들어야한다.
즉, 트리에서 가장 긴 경로는 트리의 지름이다. 트리의 지름은 트리 내에서 두개의 정점 사이의 가장 긴 경로이다.하지만 위에서 말했듯이 우리는 문제를 해결하기 위해 A-B,A-C,C-B의 거리 중 최소한 2개를 가장 크게 만들어야한다고 했으므로 트리의 지름이 2개가 있어야 한다.
따라서 이 문제를 해결하기위해서 첫번째로 찾아야할 것이 트리의 지름이 2개이상인지 확인하고 2개이상이라면중간값은 무조건 트리의 지름이다.
하지만 트리의 지름이 트리 내에 1개만 존재한다면 어떤 답이 나와야할까.이 문제에서는 정점3개를 고르기때문에 트리의 지름을 이루는 경로에서 양 끝 정점 A,B라고 하고 나머지 정점이 C라면
f(A,B,C)는 (A-C, B-C, 트리의지름(A-B)) 이므로 A-C, B-C중 하나를 최대로 만들어주면 된다.
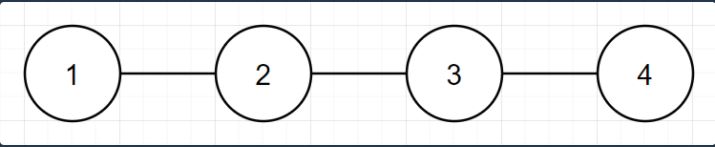
간단히 말해서 문제에서 친절하게 주어진 예시에서 트리의 지름을 이루는 양 정점이 1, 4 이고 나머지 한 정점은 트리의 지름을 이루는 양 정점의 인접한 정점을 골라주면 된다.
이때의 중간값은 항상 트리의 지름-1 을 보장할 수 있다.
이는 우리가 '중간값'을 구하기 때문에 이러한 접근법으로 쉽게 해결할 수 있었다.
- 소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
#include <string>
#include <vector>
#include <unordered_map>
#include <iostream>
using namespace std;
unordered_map<int,vector<int> > trees;
unordered_map<int,vector<int> > tree_length;
bool visit[250002];
int max_step=-1;
void find_path(int vertex,int step) {
visit[vertex]=true;
if(max_step<=step) {
max_step=step;
tree_length[max_step].push_back(vertex);
}
for(int i=0;i<trees[vertex].size();i++) {
if(!visit[trees[vertex][i]]) {
find_path(trees[vertex][i],step+1);
}
}
visit[vertex]=false;
}
int solution(int n, vector<vector<int>> edges) {
int answer = 0;
int x,y,next_v;
for(int i=0;i<edges.size();i++) {
x=edges[i][0];
y=edges[i][1];
trees[x].push_back(y);
trees[y].push_back(x);
}
find_path(1,0); // 1:임의의 한점에서 가장 먼 정점 A을 찾는다.
for(int i=0;i<2;i++) {
// 1에서 찾은 정점 A에서 다시 또 그 점에서 가장 먼 정점 B들을 찾는다.
next_v=tree_length[max_step][0];
max_step=-1;
tree_length.clear();
find_path(next_v,0);
if(tree_length[max_step].size()>1) return max_step; // 가장 먼 정점(트리의 지름)이 2개이상이면 중간값 확정
// 1개라면 한번 더 정점B에 대해서 가장 먼 정점 C들을 찾아본다.
}
return max_step-1; // 2번 시도에도 정점이 1개만 나오면 트리의 지름은 1개
}
|
cs |
'Problem Solving > 프로그래머스' 카테고리의 다른 글
| [C/C++] Lv3 프로그래머스 - 외벽 점검 (0) | 2021.01.14 |
|---|---|
| [C/C++] Lv3 프로그래머스 - 징검다리 건너기 (0) | 2021.01.12 |
| [C/C++] Lv3 프로그래머스 - 경주로 건설 (0) | 2021.01.11 |
| [C/C++] Lv4 프로그래머스 - 지형 편집 (0) | 2021.01.10 |
| [C/C++] Lv4 프로그래머스 - 지형 이동 (0) | 2021.01.10 |
- Total
- Today
- Yesterday
- cnn
- 프로그래머스
- ResNet
- 네트워킹데이
- Unet
- 부스트캠프 AI Tech
- DeepLearning
- 동적계획법
- 백준
- 공공데이터
- 다이나믹프로그래밍
- 백트래킹
- 데이터연습
- Unet 구현
- python
- 그리디
- 코딩테스트
- 알고리즘
- dfs
- 브루트포스
- pandas
- Vision AI 경진대회
- 이분탐색
- P-Stage
- NLP 구현
- C++
- DACON
- AI 프로젝트
- Data Handling
- 데이터핸들링
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
