티스토리 뷰
[Day 07] 경사하강법
1. 강의 복습 내용
경사하강법
1. 미분
- 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에 제일 많이 사용하는 기법
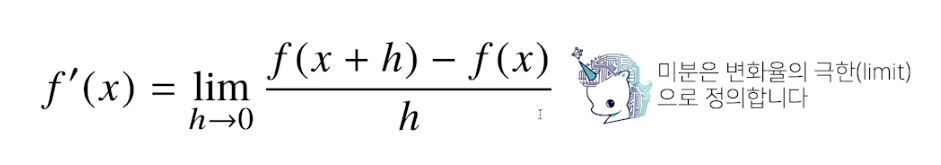
import sympy as sym
from sympy.abc import x
sym.diff(sym.poly(x**2+2*x+3),x)
#Poly(2*x+2,x,domain='ZZ')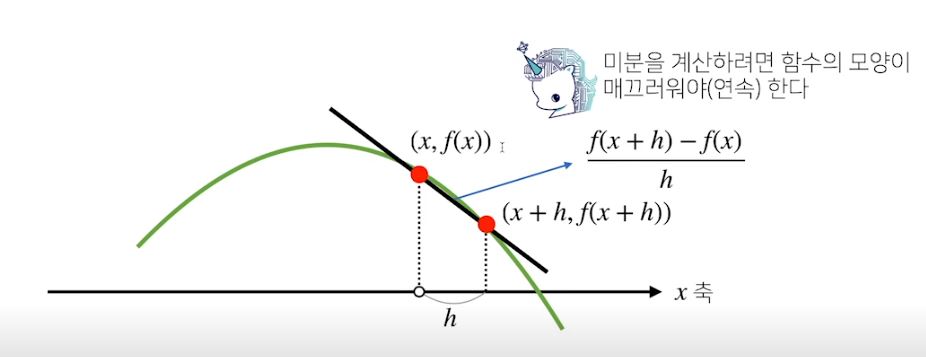
- 한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수값이 증가/감소하는지 알 수 있다.
- 미분값을 빼면 경사하강법(Gradient descent)이라 하며 함수의 극소값의 위치를 구할 때 사용한다.
- 미분값을 더하면 경사상승법(Gradient ascent)이라 하며 함수의 극대값의 위치를 구할 때 사용한다.
- 이렇듯, 경사하강/상승법은 극값에 도달하면 움직임을 멈춘다.
# Input: gradient, init, lr, eps
# Output : var
# gradient : 미분을 계산하는 함수
# init : 시작점
# lr : 학습률
# eps : 알고리즘 종료조건
var=init
grad=gradient(var)
while (abs(grad)>eps) :
var = var -lr * grad
grad=gradient(var)2. 벡터의 미분
- 벡터가 입력인 다변수 함수의 경우 편미분(partial differentiation)을 사용한다.
- 각 변수 별로 편미분을 계산한 그레디언트(gradient) 벡터를 이용하여 경사하강/상승법에 사용할 수 있다.
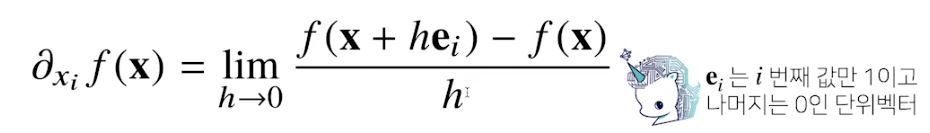
import sympy as sym
from sympy.abc import x, y
sym.diff(sym.poly(x**2+2*x*y+3)+sym.cos(x+2*y),x)
# 2*x + 2*y - sin(x+ 2*y)
3. 경사하강법 알고리즘의 이용
- 선형회귀분석
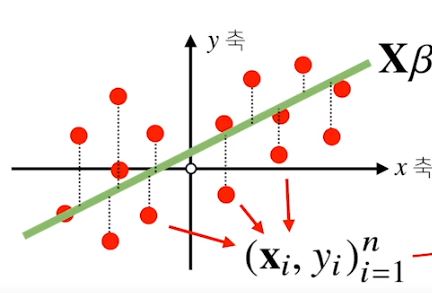
우리는 전날에 선형회귀분석을 무어-펜로즈 역행렬을 이용하여 목적식을 구하였다.
하지만 선형모델이 아닌 다른모델을 분석할때는 일반적으로 경사하강법 알고리즘을 사용하므로 우리는 경사하강법을 알아야 한다.
* 목적식을 최소화하는 β를 구하는 경사하강법 알고리즘
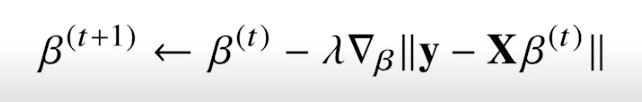
4. 경사하강법의 한계
- 이론적으로 경사하강법은 미분가능하고 볼록(convex)한 함수에 대해선 적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장되어 있다.
- 특히 선형회귀의 경우 목적식은 회귀계수에 대해 볼록함수이기 때문에 알고리즘을 충분히 돌리면 수렴이 보장된다.
- 하지만 비선형회귀 문제의 경우, 목적식이 무조건 볼록하지 않으므로 수렴이 항상 보장되지 않는다.
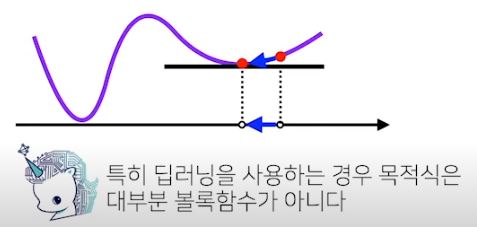
5. 확률적 경사하강법
- 위의 한계를 대체하기 위해 확률적 경사하강법(SGD, Stochastic Gradient Descent)을 사용
- 볼록이 아닌 목적식은 SGD를 통해 최적화할 수 있으므로 머신러닝 학습에 더 효율적이다.
우리가 모든 데이터 세트를 가지고 모델을 학습 시킨다면 예측의 정확성은 높일 수 있으나, 매우 오랜 시간이 걸릴 것이다. 확률적 경사하강법은 랜덤으로 단 한 개의 데이터를 추출하여(Batch 크기 = 1) 기울기를 얻어 낸다.
이러한 과정을 반복 학습하여 최적점을 찾아내는 것이 확률적 경사하강법이다.
| 경사하강법 | 확률적 경사하강법 | |
| 1회 학습에 사용되는 데이터 | 모든 데이터 | 랜덤으로 추출된 1개의 데이터 |
| 정확도 | 학습횟수에 비례 | 학습횟수에 비례 |
| 노이즈 | 거의 없다. | 비교적 크다. |
| 해를 찾는 과정 |  |
 |
- 한 번 학습마다 모든 데이터를 계산하여 최적의 다음 스텝으로 나아가는 경사하강법과 달리, 확률적 경사하강법은 랜덤하게 추출한 하나의 데이터만 계산하여 빠르게 다음 스텝으로 넘어간다. 그 결과 더 빠르게 최적점을 찾을 수 있게 되었지만, 그 정확도는 낮아진다.
* Batch(배치)란?
배치란, 단일 반복에서 기울기를 계산하는 데 사용하는 예의 총 개수
즉 한번 학습에 사용되는 데이터 = 배치의 크기
* Epoch란?
전체 data set에 대해 학습을 완료한 상태
즉, 1 epoch는 전체 데이터 셋에 대해 한번 학습을 완료한 상태
5-1) 미니 배치 확률적 경사하강법(Mini-batch SGD)
- 확률적 경사하강법의 한계를 보완하다
확률적 경사하강법은 단일 반복에서 기울기를 구할 때 사용되는 데이터가 1개이므로, 노이즈가 너무 심하다는 한계가 있었다.
이를 보완하는 것이 미니 배치 확률적 경사하강법(Mini-Batch SGD)이다.
미니 배치 확률적 경사하강법은 전체 배치 반복과 SGD 간의 절충안으로써 배치의 크기가 2~100사이로 설정한다.
미니 배치 확률적 경사하강법은 SGD의 노이즈를 줄이면서도 전체 배치보다는 더 빠르게 최적점을 구할 수 있다.
https://brunch.co.kr/@linecard/561
https://codingrabbit.tistory.com/12
2. 피어 세션
1. 강의 내용 리뷰
2. Further question 집단 지식으로 해결하기(*****)
- 경사하강법으로 선형회귀 계수구하기 식 미분 과정 전개, 이해하기
3. Conclusion
오늘 피어세션은 대부분의 시간을 다같이 머리를 싸매고 미분 과정을 이해하는 것에 사용했다.
오랜만에 수학기호, 수식들을 파해치려니 머리가 아프다.
경사하강법의 경우 BAT 대비하면서 선행을 했었던 기억이 있어서 개념적으로 이해하기는 어려움이 없었는데
미분은 언제나 머리가 아프다
'부스트캠프 AI Tech > 학습정리' 카테고리의 다른 글
| [Day 09] Pandas / 통계학 (0) | 2021.01.28 |
|---|---|
| [Day 08] Pandas / 딥러닝 학습방법 이해하기 (0) | 2021.01.27 |
| [Day 06] Numpy / 벡터 / 행렬 (0) | 2021.01.25 |
| [Day 05] 파이썬으로 데이터 다루기 (0) | 2021.01.22 |
| [Day 04] 파이썬 기초 문법 3 (0) | 2021.01.21 |
- Total
- Today
- Yesterday
- 그리디
- 이분탐색
- 데이터핸들링
- P-Stage
- 코딩테스트
- dfs
- 데이터연습
- NLP 구현
- DACON
- 브루트포스
- cnn
- Unet 구현
- 알고리즘
- python
- Data Handling
- ResNet
- DeepLearning
- 네트워킹데이
- 동적계획법
- 백준
- C++
- pandas
- Unet
- 백트래킹
- 다이나믹프로그래밍
- 프로그래머스
- 공공데이터
- Vision AI 경진대회
- 부스트캠프 AI Tech
- AI 프로젝트
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
