티스토리 뷰
[Day 06] Numpy / 벡터 / 행렬
1. 강의 복습 내용
Numpy
- Numpy는 파이썬으로 진행되는 모든 데이터 분석과 인공지능 학습에 있어 가장 필수적으로 이해해야 하는 도구
- Numpy는 Numerical Python의 약자로 일반적으로 과학계산에서 많이 사용하는 선형대수의 계산식을 파이썬으로 구현할 수 있도록 도와주는 라이브러리
1. Numpy 사용해보기
import numpy as np
test_array=np.array([1,2,3,4],float)Numpy는 변수선언을 꼭 해줘야한다. C기반으로 작성되있기 때문에 동적타이핑 언어를 지원하지 않는다.
a=[[1,2,3],[4,5,6],[4,5,6]]
print(np.array(a).shape)
# (3,3)a=[1,2,3,4,5,6,7,8]
print(np.array(a).reshape(2,-1))
# array([[1, 2, 3, 4], [5, 6, 7, 8]])
print(np.array(a).reshape(2,2,-1))
# array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])이런식으로 shape의 변환도 자유롭게 가능하다. 단, 요소의 개수가 변환할 shape에 1:1 매칭이 가능해야함
2. Flatten
- 다차원 array를 1차원 array로 변환
a=[[1,2,3],[4,5,6],[7,8,9]]
np.array(a).flatten()
# array([1, 2, 3, 4, 5, 6, 7, 8, 9])3. Indexing, slicing
a=np.array([[1,2,3,4,5],[6,7,8,9,10]],int)
print(a)
# array([[ 1, 2, 3, 4, 5], [ 6, 7, 8, 9, 10]])
print(a[:,2:])
# array([[ 3, 4, 5], [ 8, 9, 10]])
print(a[1,1:])
# array([ 7, 8, 9, 10])
print(np.arange(100).reshape(10,-1))
# arange
'''
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
[20, 21, 22, 23, 24, 25, 26, 27, 28, 29],
[30, 31, 32, 33, 34, 35, 36, 37, 38, 39],
[40, 41, 42, 43, 44, 45, 46, 47, 48, 49],
[50, 51, 52, 53, 54, 55, 56, 57, 58, 59],
[60, 61, 62, 63, 64, 65, 66, 67, 68, 69],
[70, 71, 72, 73, 74, 75, 76, 77, 78, 79],
[80, 81, 82, 83, 84, 85, 86, 87, 88, 89],
[90, 91, 92, 93, 94, 95, 96, 97, 98, 99]])
'''
* slicing => [ start : end : step ]
print(np.arange(0,10,0.5))
# array([0. , 0.5, 1. , 1.5, 2. , 2.5, 3. , 3.5, 4. ,
# 4.5, 5. , 5.5, 6. , 6.5, 7. , 7.5, 8. , 8.5, 9. , 9.5])4. zeros / ones
print(np.zeros(shape=(10,),dtype=np.int8))
# array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0], dtype=int8)
print(np.ones(shape=(10,),dtype=np.int8))
# array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=int8)5. identity (단위행렬) 생성
print(np.identity(n=3,dtype=np.int8))
'''
array([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]], dtype=int8)
'''6. eye (대각선의 요소가 1인 행렬) 생성
print(np.eye(3,5,k=2))
'''
array([[0., 0., 1., 0., 0.],
[0., 0., 0., 1., 0.],
[0., 0., 0., 0., 1.]])
'''eye의 경우는 k값으로 시작 index를 변경해줄 수 있다.
7. diag : 대각선 요소 값 추출 (마찬가지로 k로 인덱스 설정 가능)
Operation Function
1. Random sampling
print(np.random.normal(0,1,10).reshape(2,5))
'''
array([[ 0.28615311, 0.14945547, -2.35756229, -0.94386015, -1.00275682],
[-0.42676382, 0.74864187, 0.82831741, 0.63533144, -0.69392474]])
'''2. Axis
* (x,y) -> (axis=0,axis=1) (x,y,z) -> (axis=0,axis=1,axis=2)
test_array=np.arange(1,13).reshape(3,4)
print(test_array)
'''
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
'''
test_array.sum(axis=1), test_array.sum(axis=0)
# (array([10, 26, 42]), array([15, 18, 21, 24]))3. Concatenate
- Numpy array를 합치는(=붙이는) 함수

4. Element-wise Operations
A=np.array([[1,2,3],[3,4,5],[4,5,6]])
B=np.array(([1,2,3],[3,4,5],[4,5,6]))
print(A*B)
'''
array([[ 1, 4, 9],
[ 9, 16, 25],
[16, 25, 36]])
'''*) A*B는 행렬의 곱셈이 아니라 단순 같은 위치에 있는 요소들의 곱
5. Dot product (@)
test_a=np.arange(1,7).reshape(2,3)
test_b=np.arange(7,13).reshape(3,2)
print(test_a.dot(test_b))
'''
array([[ 58, 64],
[139, 154]])
'''6. Transpose (= 전치행렬)
test_a=np.arange(1,7).reshape(2,3)
print(test_a)
'''
array([[1, 2, 3],
[4, 5, 6]])
'''
print(test_a.transpose())
'''
array([[1, 4],
[2, 5],
[3, 6]])
'''
print(test_a.T)
'''
array([[1, 4],
[2, 5],
[3, 6]])
'''7. Broadcasting
- Shape가 다른 행렬 간 연산을 지원
test_matrix=np.array([[1,2,3],[4,5,6]],float)
scalar=3
print(test_matrix+scalar)
'''
array([[4., 5., 6.],
[7., 8., 9.]])
'''
vector=[2,3,4]
print(test_matrix+vector)
'''
array([[ 3., 5., 7.],
[ 6., 8., 10.]])
'''8. ALL / ANY
ANY - 하나라도 조건에 만족 시 True
ALL - 모두 조건에 만족 시 True
a=np.arange(10)
# array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
print(np.all(a<10))
# True
print(np.any(a<1))
# True
9. np.where
*) 조건에 맞는 index를 반환
a=np.arange(10)
print(np.where(a>5))
# (array([6, 7, 8, 9], dtype=int64),)10. argmax / argmin / argsort

11. Boolean index / fancy index
 |
 |
* Boolean index VS fancy index
- boolean index : boolean list
- fancy index : integer list
- boolean index : shape이 같아야한다
- fancy index : 안같아도 되지만 인덱스크기범위를 넘어가면 안된다
Math : 벡터
- 벡터는 숫자를 원소를 가지는 리스트 또는 배열
- 벡터는 공간에서 한점을 나타낸다
- 벡터는 원점으로부터 상대적 위치를 표현
- 벡터에 숫자를 곱해주면 길이만 변한다
- 벡터끼리 같은 모양을 가지면 덧셈, 뺄셈을 계산할 수 있다.
- 벡터끼리 같은 모양을 가지면 성분곱을 계산할 수 있다.
1. 벡터의 노름
- 원점으로부터의 거리
1) L1 노름
- 각 성분의 변화량의 절대값을 모두 더한다
2) L2 노름
- 피타고라스 정리를 이용하여 유클리드 거리를 계산한다.
* 노름의 종류에 따라 기하학적 성질이 달라진다.
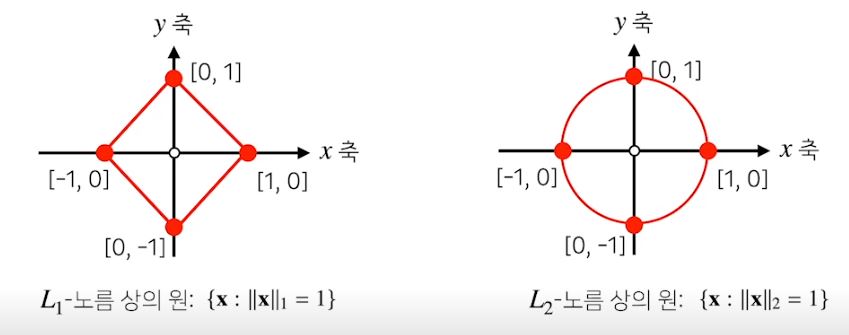
2. 두 벡터 사이의 거리
- L1, L2 노름을 이용하여 두 벡터 사이의 거리를 계산할 수 있다.
- 두 벡터 사이의 거리를 계산할때는 벡터의 뺄셈을 이용
3. 두 벡터 사이의 각도
- 제2 코사인 법칙에 의해 두 벡터 사이의 각도를 구할 수 있다.
- 분자를 쉽게 계산하는 방법 : 내적

4. 벡터의 내적
- 내적은 정사영된 벡터의 길이와 관련이 있다.
- Proj(x) = || x || cos(세타)
- 내적은 정사영의 길이를 벡터 y의 길이 || y || 만큼 조정한 값
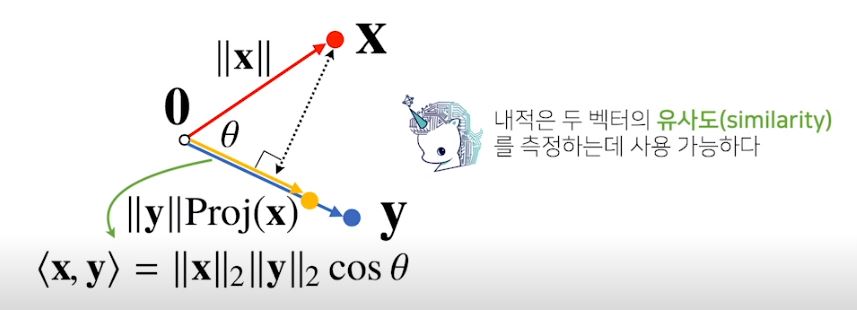
* 내적 구하는 2가지 방법
1) 요소의 곱
2) 벡터의 크기 * 벡터의 각도
이를 이용하여 벡터의 각도를 구할 수 있다.
Math : 행렬
1. 역행렬 ( N*N)
: determinant가 0 이 아닌 경우 구할 수 있다.
-> N*N이 아니거나, determinant=0이여도 '유사 역행렬'로 구할 수 있다.
np.linalg.inv
* 유사 역행렬
1) 유사 역행렬
2) 푸어-펜로즈 ( n>=m , n<=m )
np.linalg.pinv2. 항등행렬 (I)
: 대각선 요소가 1이고 나머지가 0인 행렬
3. 전치행렬 (A^T)
: 행과 열을 교환하여 얻은 행렬 (=numpy 에서 transpose)
2. 피어 세션
1. 강의 관련 토의
- 유사 역행렬 Shape가 변하는 의미가 무엇일까? 표면적인 부분말고 더 있는지 DFS 식 토의 진행
- 벡터의 내적 Proj(x)의 의미 및 증명 -> 단위 벡터같은 역할인가? -> DFS 식 토의 진행
- 전체적인 강의 내용 Review (Numpy -> Math(벡터,행렬))
- 오늘 배운 강의 내용으로 코어타임 이후 학습해볼 것
- 수학 관련 추천 사이트 공유 (시각화 좋은 위주로)
2. 오늘 배운 역행렬에서 더 나아가 학습해보자
9254번: 역행렬
\(A\)의 역행렬이 존재하면 \(N\)개의 줄에 걸쳐 \(A^{-1}\)의 정보를 출력한다. 실수가 될 수 있기 때문에, 10-6 이내의 절대/상대 오차 범위 내에 있어야 정답으로 처리된다. 만약, 역행렬이 존재하지
www.acmicpc.net
- N*N의 역행렬을 구하는 과정을 직접 코딩해보자.
3. 행렬의 곱셈 (Numpy)을 활용하여 아주 큰수의 행렬 제곱을 구해보자.
10830번: 행렬 제곱
크기가 N*N인 행렬 A가 주어진다. 이때, A의 B제곱을 구하는 프로그램을 작성하시오. 수가 매우 커질 수 있으니, A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
- 행렬의 곱셈을 직접 구현해보자(N^3 직접 구현 or Numpy 연산 활용)
3. Conclusion
오늘부터 AI를 위한 수학 강의가 시작되었다.
더 불어 이 수학을 이용하는 라이브러리들도 배우기 시작했는데, 오늘은 Numpy로 기존에 Matlab을 대체하는 라이브러리를 처음 배웠다.
다양한 수학적 기능을 지원하는 것이 내부 코드가 궁금해졌다. 특히 역행렬과 유사역행렬을 구하는 로직이 참 궁금해졌다.
다행히 Numpy는 C로 구현되어있어서 파이썬과 다른 부분이 있었는데 별 어려움없이 이해할 수 있었다.
역시 성능은 C인가..
본격적으로 수학을 배우기 시작하는데, 코딩만 하다가 수학을 잡으니까 머리가 아프다. 차근 차근 정리하면서 배운 수학들을 어떻게 하면 코딩에 옮기면서 익혀볼 지 고민해야겠다.
'부스트캠프 AI Tech > 학습정리' 카테고리의 다른 글
| [Day 08] Pandas / 딥러닝 학습방법 이해하기 (0) | 2021.01.27 |
|---|---|
| [Day 07] 경사하강법 (0) | 2021.01.26 |
| [Day 05] 파이썬으로 데이터 다루기 (0) | 2021.01.22 |
| [Day 04] 파이썬 기초 문법 3 (0) | 2021.01.21 |
| [Day 03] 파이썬 기초 문법 2 (0) | 2021.01.20 |
- Total
- Today
- Yesterday
- DACON
- python
- Unet 구현
- C++
- 데이터연습
- 다이나믹프로그래밍
- AI 프로젝트
- 알고리즘
- 백트래킹
- NLP 구현
- dfs
- Data Handling
- 데이터핸들링
- Vision AI 경진대회
- P-Stage
- DeepLearning
- 그리디
- pandas
- 프로그래머스
- 부스트캠프 AI Tech
- 동적계획법
- Unet
- cnn
- 브루트포스
- 이분탐색
- 공공데이터
- 네트워킹데이
- ResNet
- 백준
- 코딩테스트
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
