티스토리 뷰
[Day 22] 페이지랭크 & 전파 모델
1. 강의 복습 내용
1.1) 페이지랭크
페이지랭크
1. 페이지랭크
1.1) 웹과 그래프
웹은 웹페이지와 하이퍼링크로 구성된 거대한 방향성이 있는 그래프로 표현 가능
웹페이지 = 정점(Vertex, Node)
하이퍼링크 = 해당 웹페이지에서 나가는 간선(Edge)
웹페이지는 추가적으로 Keyword 정보를 담고 있다.
1.2) 구글 이전의 검색 엔진
- 첫번째 시도
웹을 거대한 디렉토리로 정리 및 표현
그러나, 웹페이지가 많아질수록 디렉토리도 깊어지고 양을 감당할 수 없게 됨
또한 카테고리 구분이 모호한 경우가 많아 저장과 검색의 어려움
- 두번째 시도
사용자가 입력한 키워드에 대해, 해당 키워드를 여러번 포함한 웹페이지를 반환
그러나, 악의적인 웹페이지에 취약한 문제 (= 일부러 거짓 키워드를 포함하여 접근을 유도할 수 있음)
*) 따라서 이러한 문제점을 보완하여 제시한 것이 '페이지랭크' 알고리즘
1.3) 페이지 랭크의 정의
- 투표 관점
페이지 랭크의 핵심 아이디어는 '투표'
투표를 통해 사용자 키워드와 관련성이 높고 신뢰할 수 있는 웹페이지를 찾는다.
웹페이지가 A가 웹페이지 B로의 하이퍼링크를 포함하고 있다면, A 작성자가 판단하기에 B가 관련성이 높고 신뢰할 수 있다는 것을 의미할 수 있다. (=A가 B에 투표했다, A와 B가 간선으로 이루어졌다(인용하였다))
이는 논문 CASE에서도 비슷하듯이, 사람들은 많이 인용된 논문을 더 많이 신뢰한다.
하지만, 단순히 투표 관점으로만 본다면 이역시도 악용될 소지가 있다. (들어오는 간선의 수만 세는 것 이므로)
-> 인위적으로 웹페이지를 만들어 하이퍼링크를 집중시켜 신뢰도 있는 페이지처럼 둔갑할 수 있다.
따라서 이를 보완하기 위해 합리적인 '가중 투표'라는 개념을 추가
즉, 관련성이 높고 신뢰할 수 있는 웹페이지의 투표를 더욱 더 중요하게 간주한다.
반면, 그렇지 않은 웹페이지의 투표는 덜 중요하게 간주
따라서 웹페이지에서 측정된 관련성과 신뢰성을 하이퍼링크로 연결된 다른 웹페이지의 관련성과 신뢰성을 구하기 위한 입력값으로 쓰이는 '재귀(Recursion)' 알고리즘을 기반으로 작동한다.
측정하려는 웹페이지의 관련성 및 신뢰도 = 페이지랭크 점수
각 웹페이지는 하이퍼링크로 연결된 나가는 이웃(그래프 상에서의 나가는 간선)에게
자신의 페이지랭크 점수 / 나가는 간선의 수(이웃의 수) 만큼의 가중치로 투표를 한다.
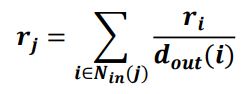
- 임의 보행 관점
페이지 랭크는 임의 보행(Random Walk)의 관점에서도 정의할 수 있다.
임의 보행을 통해 웹을 서핑하는 웹서퍼를 가정하고, 웹서퍼는 현재 웹페이지에 있는 하이퍼링크 중 하나를 균일한 확률로 클릭하는 방식으로 서핑한다.

웹서퍼가 이 과정을 무한히 반복한다면 (= t가 무한대로 커지면) 확률분포는 p(t)로 수렴한다.
즉, p(t) = p(t+1) = p 가 성립한다.
수렴한 확률분포 p는 정상분포(Stationary Distribution)이라고 부른다.
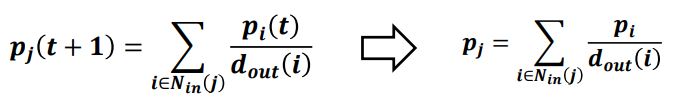
즉, 임의 보행 관점에서의 페이지랭크 수식도 t가 무한히 커진다면 결국 투표 관점에서의 페이지랭크의 수식과 같아진다.
2. 페이지랭크의 계산
- 페이지랭크 점수의 계산에는 반복곱(Power Iteration)을 사용한다.

2.1) 페이지랭크 점수 계산의 문제점
(1) 스파이더 트랩
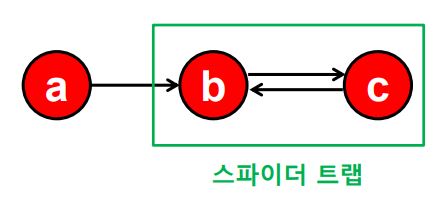
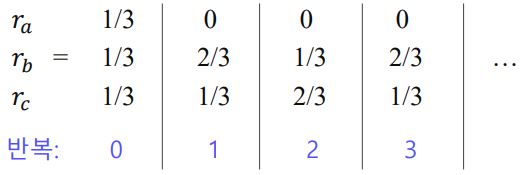
다음의 예시와 같이, 페이지랭크 점수가 수렴하지 않고 반복된다. (1->2->3->1->2->3 .... )
즉, 들어오는 간선은 있지만 나가는 간선은 없는 정점 집합인 스파이더 트랩(Spider Trap)에 의한 문제이다.
(2) 막다른 정점

다음의 예시와 같이, 페이지랭크의 점수가 0으로 수렴해버린다.
즉, 들어오는 간선은 있지만 나가는 간선은 없는 막다른 정점에 의한 문제이다.
2.2) 페이지랭크 점수 계산의 해결책
- 이와 같은 문제점(스파이더 트랩, 막다른 정점)을 해결하기 위해 순간이동(Teleport)을 도입한다.
임의 보행 관점에서, 웹을 서핑하는 웹서퍼의 행동을 다음과 같이 수정한다.
(1) 현재 웹페이지에 하이퍼링크가 없다면, 임의의 웹페이지로 순간이동한다.
(2) 현재 웹페에지에 하이퍼링크가 있다면, 앞면이 나올 확률이 a인 동전을 던진다.
(3) 앞면이라면, 하이퍼링크 중 하나를 균일한 확률로 선택해 클릭
(4) 뒷면이라면, 임의의 웹페이지로 순간이동
(1)과 (4)의 임의의 웹페이지는 전체 웹페이지들 중에 하나를 균일확률로 선택한다.
순간이동에 의해서 스파이더 트랩이나 막다른 정점에 갇히는 경우가 사라졌다.
이때 a를 감폭 비율(Damping Factor)이라고 부르며 보통 값으로 0.8 정도를 사용한다.

1.2) 전파모델
전파모델
1.1) 의사결정 기반의 전파 모형
- 주변의 의사결정들이 본인의 의사결정에 영향을 미치는 경우
- 주변 사람들의 의사결정을 고려하여 각자 의사 결정을 내리는 경우에 의사결정 기반의 전파 모형을 사용
- 가장 간단한 형태의 의사결정 기반의 전파 모형 -> '선형 임계치 모형(Linear Threshold Model)'
1.2) 선형 임계치 모형 (Linear Threshold Model)
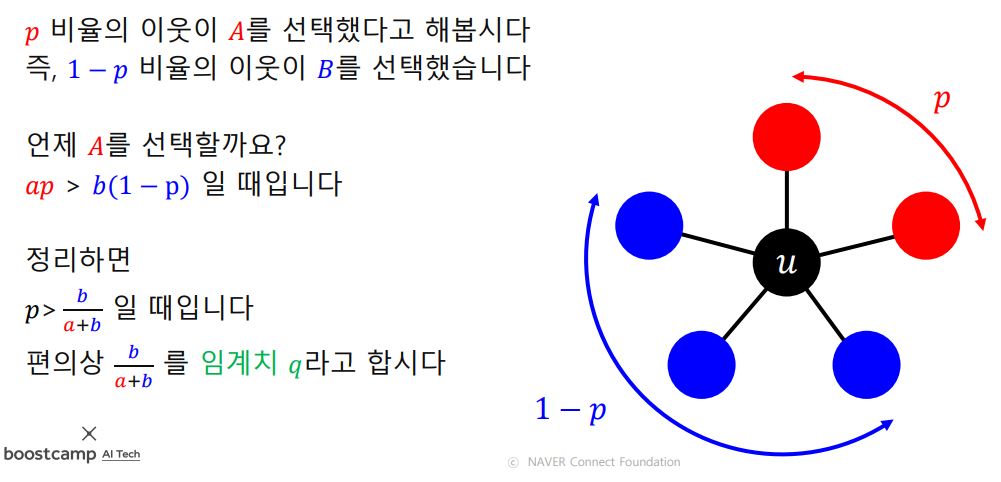
- 각 정점은 이웃 중 A를 선택한 비율이 임계치 q를 넘을 때만 A를 선택
- 이때 처음부터 A를 고수하고 있던 얼리 어답터들을 시드 집합(Seed Set)이라고 한다.
2.1) 확률적 전파 모형
전파가 각 노드의 의사결정으로 일어나는 것이 아닌 확률적 과정을 통해 일어날 때 적합한 모델
예를 들어, 코로나의 전파는 누구도 코로나에 걸리기로 '의사결정'을 내리지 않기 때문에 의사결정 기반 모형은 적합하지 않고, 확률적 과정으로 전파되기 때문에 확률적 전파 모형을 고려해야한다.
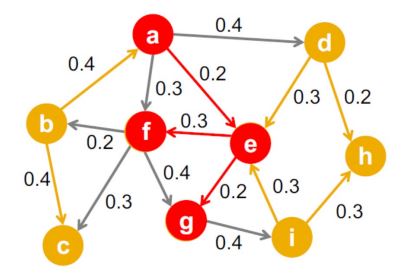
2.2) 독립 전파 모형 (Independent Cascade Model)
각 간선 (u,v)의 가중치 p는 u가 감염되었을 때 (그리고 v가 감염되지 않았을 때) u가 v를 감염시킬 확률
즉, 각 정점 u가 감염될 때 마다, 각 이웃 v는 p 확률로 전염된다.
이때 서로 다른 이웃이 전염되는 확률은 독립적이다.
독립 전파 모형은 최초 감염자들로부터 시작한다.
이전 모형과 마찬가지로 첫 감염자들을 시드 집합(Seed Set)이라고 부른다.
더이상 새로운 감염자가 없으면 종료한다.
이때 감염자는 계속 감염자 상태로 남아있는 것을 가정하는데, 감염자의 회복을 가정하는 SIS, SIR 등의 다른 전파 모형도 있다.
3.1) 바이럴 마케팅
- 바이럴 마케팅은 소비자들로 하여금 상품에 대한 긍정적인 입소문을 내게 하는 기법
- 바이럴 마케팅이 효과적이기 위해서는 소문의 시작점이 중요 (시드집합의 중요성)
- 시작점이 어디인지에 따라서 입소문이 전파되는 범위가 영향을 받기 때문
- 따라서, 소셜 인플루언서(Social Influencer)들이 높은 광고비를 받는 이유이다. (시드집합)
3.2) 시드 집합의 중요성
- 바이럴 마케팅의 경우와 마찬가지로, 전파 모형들에서도 시드 집합이 전파 크기에 많은 영향을 끼친다.
 |
 |
4) 전파 최대화 문제
- 시드 집합을 선택할 수 있다면, 어떻게 선택하는 것이 가장 전파가 잘 일어날 것인가?
- 그래프, 전파 모형 그리고 시드 집합의 크기가 주어졌을 때, 전파를 최대화하는 시드 집합을 찾는 문제를 전파 최대화(Influence Maximization) 문제라고 부른다.
- 하지만 전파를 최대화하는 시드 집합을 찾는 것은 굉장히 어려운 문제이다.
- 예를 들어, 정점이 10000개, 시드 집합의 크기가 10인 전파를 최대화하는 시드 집합을 찾기 위해서는, 경우의 수가 무려 2,743,355,077,591,282,538,231,819,720,749,000개이다.
- 즉, N! / (N-K)!K! 의 경우의수가 필요하다. (N= 정점의 수, K= 시드 집합의 크기)
4.1) 정점 중심성 휴리스틱
- 대표적 휴리스틱으로 정점의 중심성(Node Centrality)을 사용한다.
- 즉, 시드 집합의 크기가 k개로 고정되어 있을 때, 정점의 중심성이 높은 순으로 k개를 선택하는 방법
- 정점의 중심성으로는 페이지랭크 점수, 연결 중심성, 근접 중심성, 매개 중심성 등이 있다.
- 합리적이지만 최고의 시드 집합을 찾는 다는 보장이 없다.
4.2) 탐욕 알고리즘 (Greedy Algorithm)
- 탐욕 알고리즘은 시드 집합의 원소, 최초 전파자를 한번에 한 명씩 선택한다.
- 매 시행 마다, 전파를 최대화 하는 시드 노드를 하나씩 찾는다.
- K번의 시행을 하여 각 시행 단계에서의 전파를 최대화 하는 노드를 찾아 K개의 시드 집합이 된다.
- 탐욕 알고리즘은 최초 전파자 간의 조합의 효과는 고려하지않고, 근시안적으로 최초 전파자를 선택하는 과정을 반복한다.
- 독립 전파 모형의 경우에는, 탐욕 알고리즘이 이론적으로 정확도가 일부 보장된다.

즉, 탐욕 알고리즘의 최저 성능은 수학적으로 보장되어 있다.
2. 피어 세션
1. 강의에 대한 토의
- 페이지랭크 시간복잡도 O(N^2)인가? 그렇다면 이런 시간복잡도로 구글은 어떻게 빠른 검색속도를 낼 수 있었을까? -> DB에 먼저 저장을 해놓고 키워드에 맞게 출력하는가? -> 페이지랭크의 시간복잡도는 O(NM) vs O(N+M) 논쟁이 존재 -> 의사코드와는 다른 기법이 적용되었을것같다
- 전파모델 예시는 Binary Classification인데, 클래스가 3개이상인 경우 전파모델에선 어떻게 표현을 하고 수식은 어떻게 표현을 할까?
- 전파 최대화 문제 해결할 수 없을까? -> NP-Hard 문제란? -> P=NP인가? -> 양자컴퓨터가 개발된다면 모든 난제들도 브루트포스로 풀리지 않을까..?
- 전파 최대화 문제, 딥러닝으로 인간이 손수 계산할 수 있을 정도의 정점 크기의 인접행렬과 Label을 두어 충분히 학습시킨 후 인간이 계산할 수 없는 영역인 (ex: Vertex>=10000) 인접행렬을 입력으로 주었을 때 어떤 답을 내놓을까?
3. Conclusion
1. 해결해야할 것
- NLP 구현 과정 익히기 (전처리과정과 학습과정이 이해가 잘 안됨) -> Pre-trained모델을 쓸때는 따로 vocab구축안해도되는가?
- 위를 토대로 DACON Novel 작가 분류 모델 구현 완성하기 (현재 Vocab 구축까지 완성)
'부스트캠프 AI Tech > 학습정리' 카테고리의 다른 글
| [Day 24] 정점 표현 & 추천 시스템 (심화) (0) | 2021.02.25 |
|---|---|
| [Day 23] 군집 탐색 & 추천시스템 1 (0) | 2021.02.24 |
| [Day 21] 그래프 이론 기초 & 그래프 패턴 (0) | 2021.02.22 |
| [Day 20] Self-supervised Pre-training Models (0) | 2021.02.19 |
| [Day 19] Transformer (0) | 2021.02.18 |
- Total
- Today
- Yesterday
- NLP 구현
- 백트래킹
- Unet 구현
- 동적계획법
- 알고리즘
- dfs
- DeepLearning
- 데이터연습
- 브루트포스
- 그리디
- 공공데이터
- P-Stage
- Unet
- DACON
- ResNet
- pandas
- 데이터핸들링
- 네트워킹데이
- 부스트캠프 AI Tech
- 코딩테스트
- AI 프로젝트
- cnn
- 이분탐색
- python
- 프로그래머스
- Vision AI 경진대회
- Data Handling
- 다이나믹프로그래밍
- C++
- 백준
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
