티스토리 뷰
[Day 23] 군집 탐색 & 추천시스템 1
1. 강의 복습 내용
1.1) 군집 탐색
군집 탐색
1. 군집
1.1) 군집의 정의
군집이란 다음의 조건들을 만족하는 정점들의 집합
(1) 집합에 속하는 정점 사이에는 많은 간선이 존재
(2) 집합에 속하는 정점과 그렇지 않은 정점 사이에는 적은 수의 간선이 존재
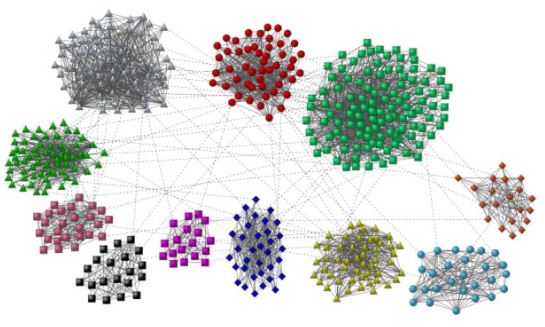
1.2) 군집 탐색 문제
그래프를 여러 군집으로 '잘' 나누는 문제를 군집 탐색(Community Detection) 문제라고 한다.
보통은 각 정점이 한 개의 군집에 속하도록 군집을 나눈다.
비지도 기계학습 문제인 클러스터링(Clustering)과 상당히 유사함
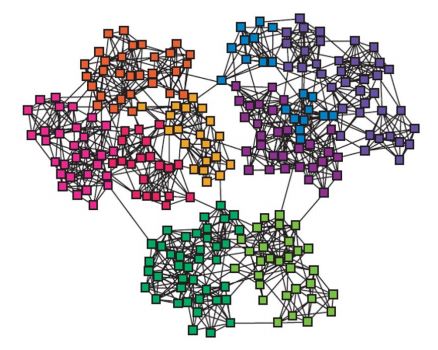
2. 군집 구조의 통계적 유의성과 군집성
2.1) 비교대상: 배치 모형
성공적인 군집 탐색을 정의하기 위해 먼저 배치 모형(Configuration Model)을 알 필요가 있음
주어진 그래프에 대한 배치 모형은 1) 각 정점의 연결성(Degree)을 보존한 상태에서 2) 간선들을 무작위로 재배치하여서 얻은 그래프를 의미함
-> 배치 모형에서 임의의 두 정점 i와 j 사이에 간선이 존재할 확률은 두 정점의 연결성에 비례
2.2) 군집성의 정의
군집 탐색의 성공 여부를 판단하기 위해서, 군집성(Modularity)가 사용
군집성은 무작위로 연결된 배치 모형과의 비교를 통해 통계적 유의성을 판단
군집성은 항상 -1 ~ +1 사이의 값을 가진다.
보통 군집성이 0.3 ~ 0.7 정도의 값을 가질 때, 그래프에 존재하는 통계적으로 유의미한 군집들을 찾아냈다고 할 수 있다.

3. 군집 탐색 알고리즘
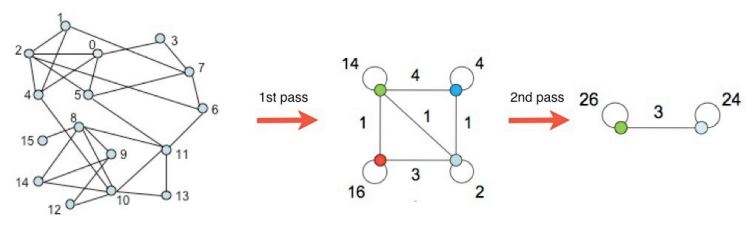
3.1) Girvan-Newman 알고리즘
- 대표적인 하향식(Top-Down) 알고리즘
- Girvan-Newman 알고리즘의 작동 과정은 다음과 같다.
1. 전체적인 그래프에서 탐색을 시작
2. 군집들이 서로 분리되도록, 매개 중심성이 높은 간선을 순차적으로 제거한다.
- 제거하는 간선은 서로 다른 군집을 연결하는 다리(Bridge) 역할을 하는 간선을 제거해야 한다.
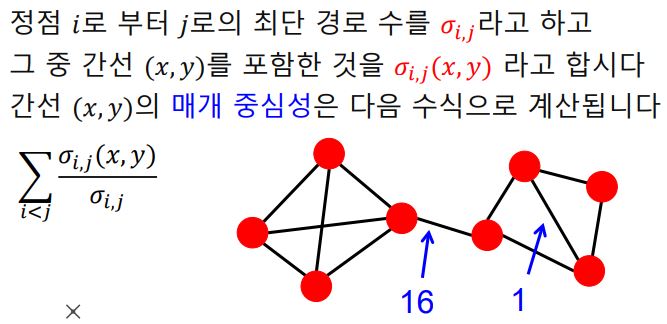
- 다리 역할을 하는 간선을 찾기 위해서는 '매개 중심성(Betweenness Centrality)'을 사용한다.
- 매개 중심성이란 해당 간선이 정점 간의 최단 경로에 놓이는 횟수를 의미한다.
3. 간선이 제거될 때 마다, 매개 중심성을 다시 계산하여 갱신한다.
4. 간선이 모두 제거될 때까지 반복한다. (매 Step마다 군집성의 변화 기록)
- 간선의 제거 정도에 따라서 다른 입도(Granularity)의 군집 구조가 나타난다.
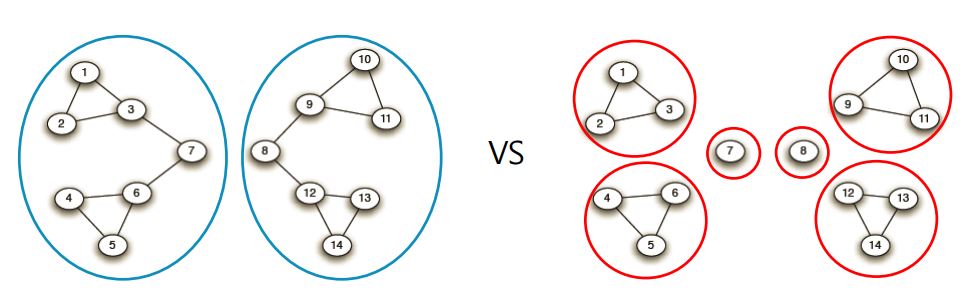
- 따라서 Girvan-Newman 알고리즘은 간선을 몇번의 Step을 거쳐 제거한 후 얻는 군집들을 선택할 지 정해야함
- 군집 탐색의 최적의 Step을 찾기 위한 방법은 다음과 같다.

- 즉, 매 Step 마다 매개 중심성이 가장 높은 간선을 제거하면서 군집성의 변화를 기록한 후 군집성이 가장 커지는 상황을 복원할 수 있다.
3.2) Louvain 알고리즘
- 대표적인 상향식(Bottom-Up) 군집 탐색 알고리즘
- Louvain 알고리즘의 작동 과정은 다음과 같다.
1) 개별 정점으로 구성된 크기 1의 군집들로 시작한다.
2) 각 정점을 기존 혹은 새로운 군집으로 이동시킨다. (이 때, 군집성이 최대화되도록 군집을 결정)
3) 더이상 군집이 증가하지 않을 때까지 2)를 반복한다.
4) 각 군집을 하나의 정점으로하는 군집 레벨의 그래프를 얻은 뒤, 3)을 수행한다.
5) 한 개의 정점이 남을 때 까지 4)를 반복한다.
4. 중첩이 있는 군집 탐색
4.1) 중첩이 있는 군집 구조
- 실제 그래프의 군집들은 중첩이 되어 있는 경우가 많다.
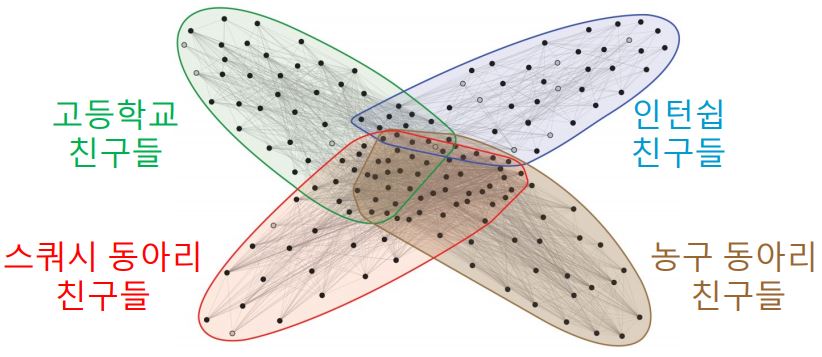
- 그러나 앞서 살펴본, 두 알고리즘 Girvan-Newman, Louvain은 군집 간의 중첩이 없다고 가정하였기 때문에 중첩이 있는 군집을 찾아낼 수 없다.
4.2) 중첩 군집 모형
- 이를 위해 아래와 같은 중첩 모형을 가정한다.
1) 각 정점은 여러 개의 군집에 속할 수 있다.
2) 각 군집 A에 대하여, 같은 군집에 속하는 두 정점은 P_{A}의 확률로 간선으로 직접 연결된다.
3) 두 정점이 여러 군집에 동시에 속할 경우 간선 연결 확률은 독립적이다.
(두 정점이 군집 A와 B에 동시에 속할 경우, 두 정점이 간선으로 직접 연결될 확률은 1-(1-P_{A})(1-P_{B})이다.
4) 어느 군집에도 함께 속하지 않는 두 정점은 낮은 확률 e으로 직접 연결된다.
- 중첩 군집 모형이 주어진다면, 주어진 그래프의 확률을 계산할 수 있다.
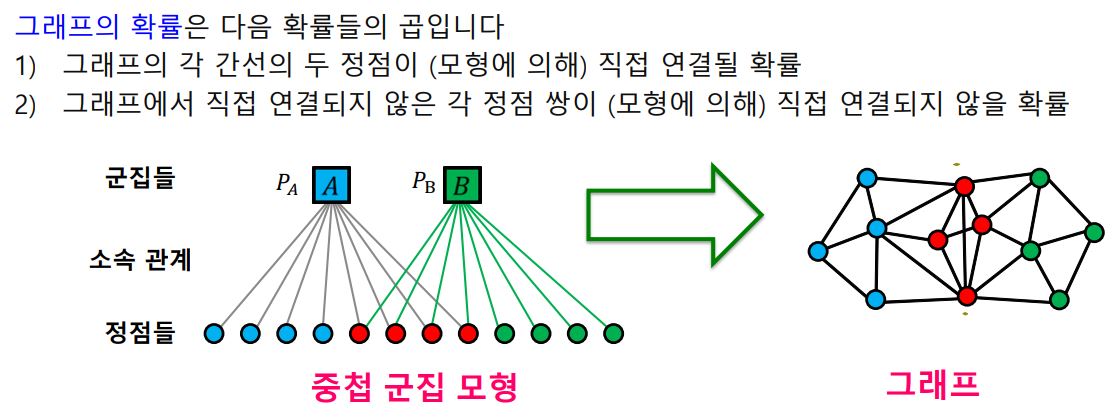
- 반대로 중첩 군집 탐색은 주어진 그래프의 확률을 최대화하는 중첩 군집 모형을 찾는 과정이다.
- 즉, 최우도 추정치(Maximum Likelihood Estimate)를 찾는 과정이다.
- 따라서 그래프를 통해 역으로 중첩 군집 모형을 찾아낼 수 있다.
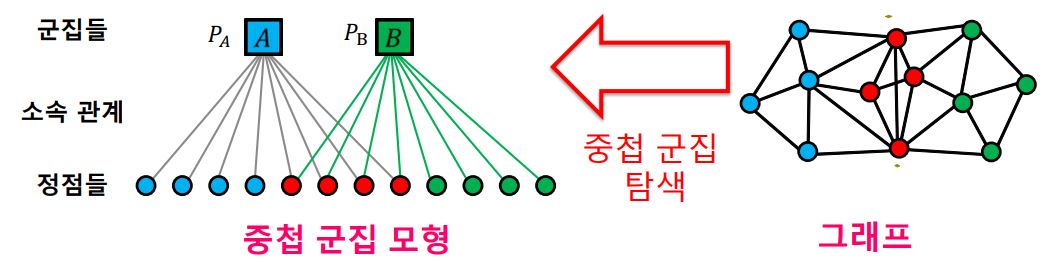
- 보다 더 중첩 군집 탐색을 용이하게 하기 위해 완화된 중첩 군집 모형을 사용한다.
- 완화된 중첩 군집 모형에서는 각 정점이 각 군집에 속해 있는 정도를 실숫값으로 표현한다.
- 이로써, 기존 모형에서는 각 정점이 각 군집에 속하거나 속하지 않거나 둘 중 하나였지만, 중간 상태를 표현할 수 있게 되었다.
- 또한, 모형의 매개변수들이 실수 값을 가지기 때문에 익숙한 최적화 도구 (경사하강법 등)을 사용하여 모형을 탐색할 수 있다.
1.2) 추천 시스템 (기초)
추천 시스템 (기초)
1. 내용 기반 추천시스템
1.1) 내용 기반 추천시스템의 원리
- 내용 기반(Content-based) 추천은 각 사용자가 구매/만족했던 상품과 유사한 것을 추천하는 방법
- 내용 기반 추천의 네 가지 단계
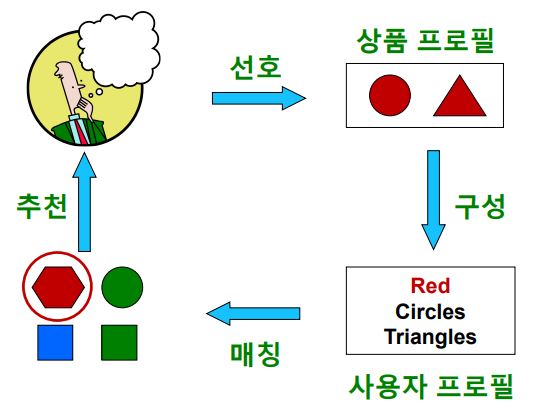
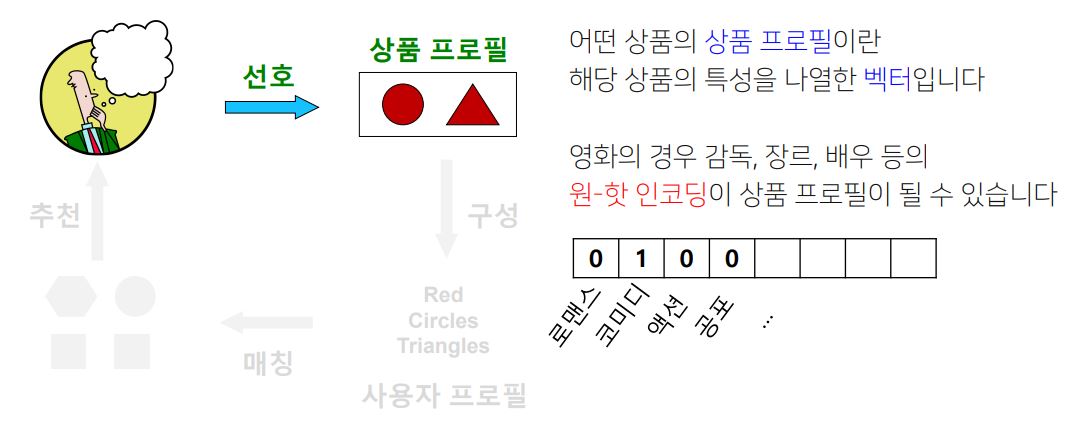
1. 사용자가 선호했던 상품들의 상품 프로필(Item Profile)을 수집하는 단계
(상품 프로필이란, 해당 상품의 특성을 나열한 벡터 ex) 상품의 Class를 원-핫 벡터로 표현)
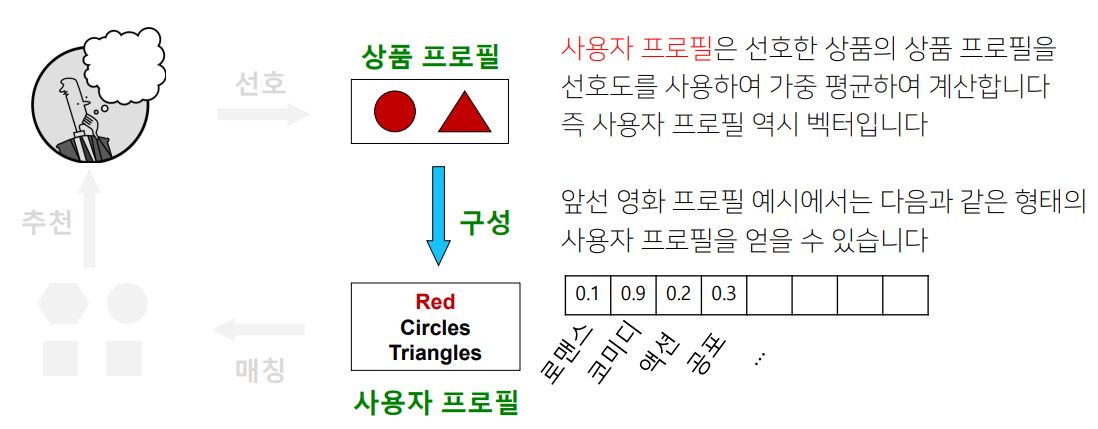
2. 사용자 프로필(User Profile)을 구성하는 단계
(사용자 프로필은 선호한 상품의 상품 프로필을 선호도를 사용하여 가중 평균한다. 이 역시 벡터이다)
3. 사용자 프로필과 다른 상품들의 상품 프로필을 매칭하는 단계
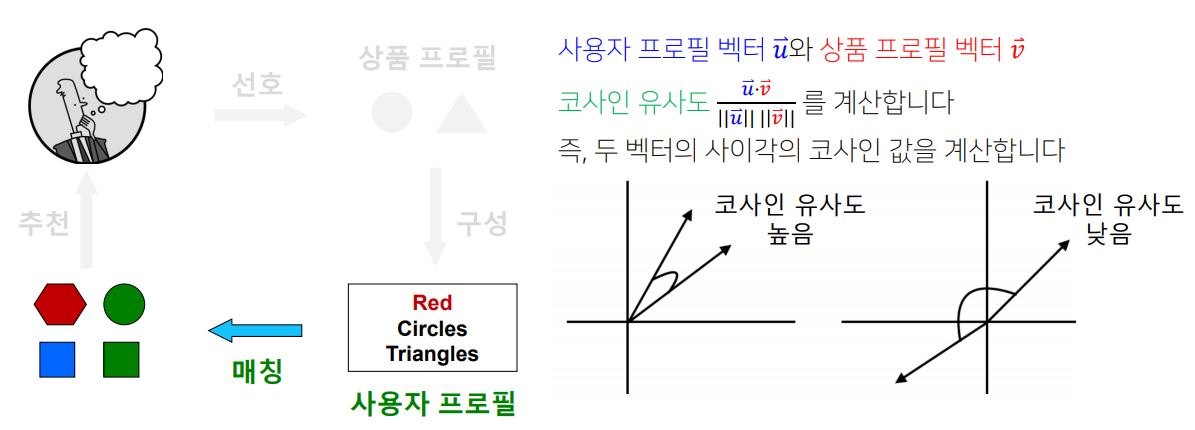
4. 사용자에게 상품을 추천하는 단계

1.2) 내용 기반 추천시스템의 장단점
1. 장점
- 다른 사용자의 구매 기록이 필요하지 않다.
- 독특한 취향의 사용자에게도 추천이 가능
- 새 상품에 대해서도 추천이 가능
- 추천의 이유를 제공할 수 있다.
2. 단점
- 상품에 대한 부가 정보가없는 경우에는 사용할 수 없다.
- 구매 기록이 없는 사용자에게는 사용할 수 없다.
- 과적합(Overfitting)으로 지나치게 협소한 추천을 할 위험이 있다.
2. 협업 필터링 추천 시스템
2.1) 협업 필터링의 원리
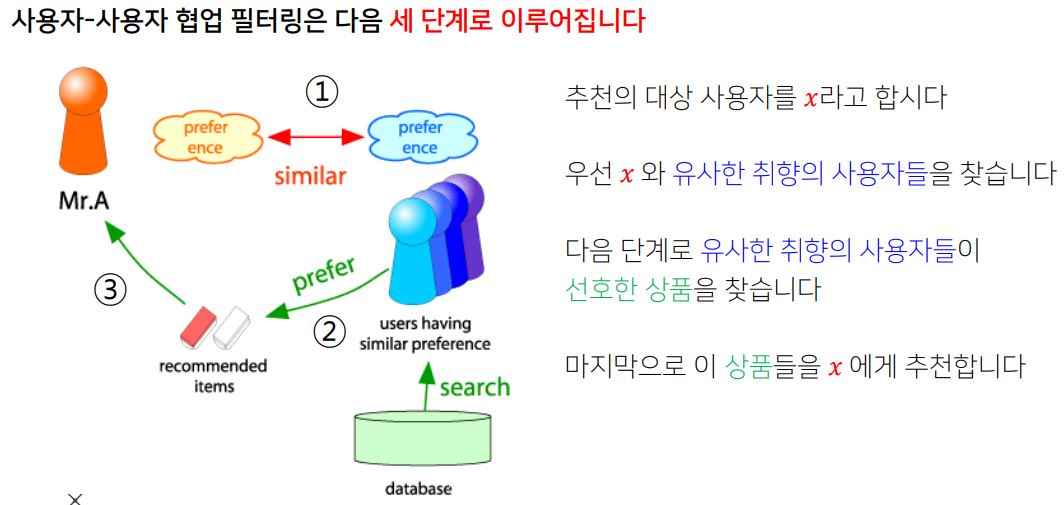
- 유사한 취향의 사용자를 찾는 방법 -> 취향의 유사도를 구할 수 있어야 한다.


- 이후 추정한 평점이 가장 높은 상품들을 추천한다.
2.2) 협업 필터링의 장단점
1. 장점
- 상품에 대한 부가 정보가 없는 경우에도 사용할 수 있다.
2. 단점
- 충분한 수의 평점 데이터가 누적되어야 효과가 있다.
- 새 상품, 새로운 사용자에 대한 추천이 불가능하다.
- 독특한 취향의 사용자에게 추천이 어렵다.
3. 추천 시스템의 평가
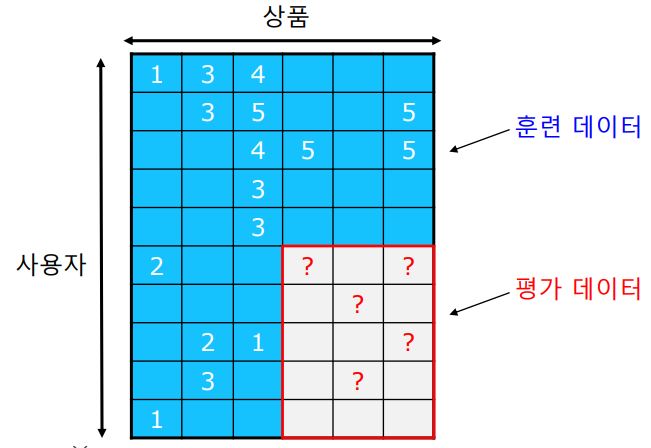
3.1) 데이터 분리
- 먼저 훈련(Training) 데이터와 평가(Test) 데이터로 분리한다.
- 이때 평가데이터의 평점은 초기화한다.
- 그 후, 훈련 데이터를 이용하여 가려진 평가 데이터의 평점을 추정한다.
- 추정한 평점과 실제 평점 데이터를 비교하여 오차를 측정한다.
3.2) 평가 지표
- 오차를 측정하는 지표로는 평균 제곱 오차(Mean Squared Error, MSE)가 많이 사용 된다.
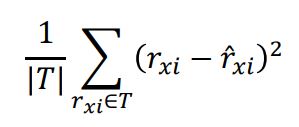
- 또 평균 제곱 오차(MSE)에 제곱근을 씌운 평균 제곱근 오차(Root Mean Squared Error, RMSE)도 많이 사용된다.
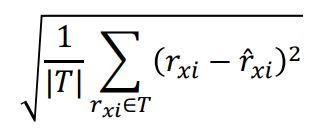
- 물론 이외에도 다양한 지표가 사용된다.
1. 추정한 평점으로 순위를 매긴 후, 실제 평점으로 매긴 순위와의 상관계수를 계산
2. 추천한 상품 중 실제 구매로 이루어진 것의 비율 측정
3. 추천의 순서 혹은 다양성까지 고려하는 지표 사용
2. 피어 세션
1. 강의에 대한 토의
- 중첩 군집 탐색에 대해 깊게 고민
- 간선이 없는 노드들의 군집 탐색 -> 클러스터링
- 내용기반, 협업필터링 추천시스템의 한계, 과연 현업에서도 사용될까?
- 딥러닝으로 추천시스템을 어떻게 고안해낼까?
3. Conclusion
오늘은 그래프의 군집 탐색 방법과 추천시스템의 기초에 대해 학습하였다.
하지만 오늘은 추천시스템이 확률적 방법에 기반한 기계학습 모델에 대해 배웠고 과연 추천시스템을 딥러닝에 어떻게 접목을 시킬 것인지 문득 궁금증이 생겼다.
그래프 이론을 딥러닝에 어떤식으로 접목될 지도 더 궁금해졌고, 추후에 배울 것이지만 미리 페이퍼들을 읽어보는 것도 나쁘지않을 것 같다.
'부스트캠프 AI Tech > 학습정리' 카테고리의 다른 글
| [Day 25] GNN (0) | 2021.02.26 |
|---|---|
| [Day 24] 정점 표현 & 추천 시스템 (심화) (0) | 2021.02.25 |
| [Day 22] 페이지랭크 & 전파 모델 (0) | 2021.02.23 |
| [Day 21] 그래프 이론 기초 & 그래프 패턴 (0) | 2021.02.22 |
| [Day 20] Self-supervised Pre-training Models (0) | 2021.02.19 |
- Total
- Today
- Yesterday
- cnn
- 코딩테스트
- dfs
- AI 프로젝트
- 공공데이터
- pandas
- DeepLearning
- 데이터핸들링
- NLP 구현
- Data Handling
- ResNet
- 그리디
- 브루트포스
- 네트워킹데이
- 알고리즘
- C++
- Unet
- 부스트캠프 AI Tech
- DACON
- 이분탐색
- 백트래킹
- 다이나믹프로그래밍
- 동적계획법
- python
- P-Stage
- 백준
- Unet 구현
- 데이터연습
- Vision AI 경진대회
- 프로그래머스
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
